Die Erfassung von Schwingungsdaten ist nur ein Teil der Herausforderung bei der Schwingungsmessung; der andere Teil ist die Analyse der resultierenden Daten. Es ist wichtig, die verschiedenen Arten von Zeitverläufen zu verstehen, die bei der Schwingungsanalyse verwendet werden, die wichtigen Unterschiede zwischen ihnen zu kennen und zu wissen, wann welche Art von Schwingungsanalysewerkzeug verwendet werden sollte. Hier ist ein kurzer Überblick über einige der Grundlagen.
Schwingungsanalyse im Zeitbereich
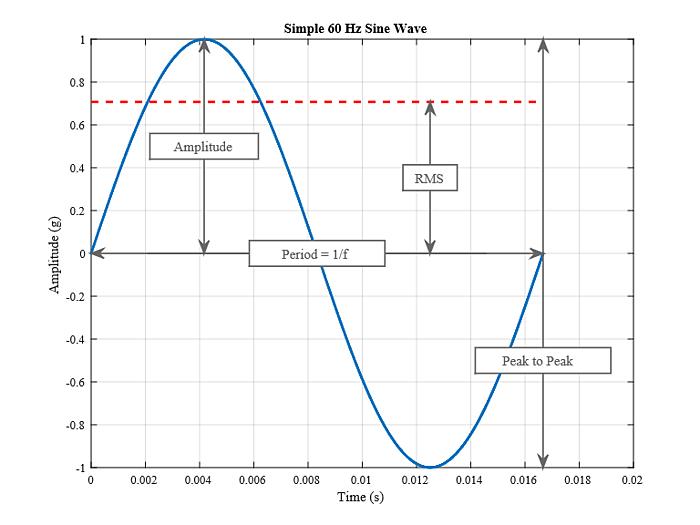
Die Schwingungsanalyse beginnt mit einem zeitlich veränderlichen realen Signal von einem Aufnehmer oder Sensor. Die Interpretation von Schwingungsdaten im Zeitbereich (Amplitude als Funktion der Zeit aufgetragen) ist bei der Bestimmung des Schwingungsniveaus auf einige wenige Parameter beschränkt: Amplitude, Spitzenwert und Effektivwert, die in einer sinusförmigen Wellenform identifiziert werden.
Der Spitzenwert oder die Amplitude ist für impulsartige Ereignisse relevant, berücksichtigt aber nicht die Dauer und damit die Energie des Ereignisses.
Dasselbe gilt für den Spitzenwert mit dem zusätzlichen Vorteil, dass er den maximalen Ausschlag der Wellenform angibt. Dies ist nützlich bei der Überprüfung von Verlagerungsinformationen, insbesondere des Spiels.
Der Effektivwert ist im Allgemeinen am nützlichsten, da er in direktem Zusammenhang mit dem Energieniveau der Schwingung und damit dem Zerstörungsgrad der Schwingung steht.
Da es sich bei Schwingungen um eine oszillierende Bewegung handelt, zielen die meisten Schwingungsanalysen darauf ab, die Geschwindigkeit dieser Schwingung oder die Frequenz zu bestimmen. Die Anzahl der Wiederholungen eines vollständigen Bewegungszyklus innerhalb einer Sekunde ist die Frequenz der Schwingung und wird in Hz gemessen. Bei einfachen Sinuswellen kann die Frequenz der Schwingung durch Beobachtung der Wellenform im Zeitbereich bestimmt werden; wenn jedoch verschiedene Frequenzkomponenten und Rauschen hinzukommen, ist eine Spektrumanalyse erforderlich, um ein klareres Bild der Schwingungsfrequenz zu erhalten.
Schwingungsanalyse im Frequenzbereich
Schnelle Fourier-Transformation (FFT)
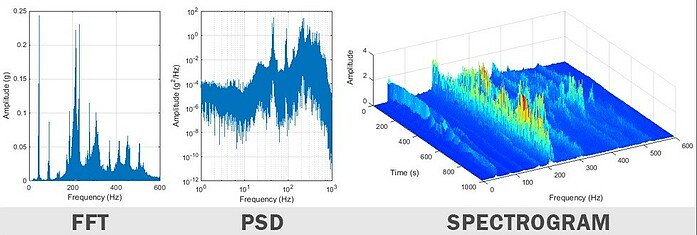
Die schnelle Fourier-Transformation (FFT) ist ein effizienter Algorithmus zur Berechnung der diskreten Fourier-Transformation (DFT). Diese Fourier-Transformation gibt die Amplitude der Schwingung als Funktion der Frequenz aus, so dass der Analysator die Ursachen der Schwingung anzeigen kann. Die Frequenzauflösung der FFT ist direkt proportional zur Signallänge und zur Abtastfrequenz. Um die Auflösung zu verbessern, muss die Aufzeichnungszeit erhöht werden, wobei jedoch auf die wechselnde Schwingungsumgebung geachtet werden muss.
Spektrogram
Das Spektrogramm nimmt eine Reihe von FFT-Spektren auf, um zu zeigen, wie sich das Spektrum (Frequenzbereich) im Laufe der Zeit verändert. Wenn die Schwingungsanalyse in einer sich verändernden Umgebung durchgeführt wird, ist das Spektrogramm ein leistungsfähiges Werkzeug, um genau zu veranschaulichen, wie sich das Schwingungsspektrum verändert.
Spektrale Leistungsdichte
Die Leistungsspektraldichte (PSD) nimmt die Amplitude der FFT, multipliziert sie mit der komplexen Konjugation und normiert sie auf die Breite des Frequenzintervalls. Dies ermöglicht einen genauen Vergleich von zufälligen Vibrationssignalen, die unterschiedliche Signallängen aufweisen. Aus diesem Grund wird die PSD in der Regel zur Beschreibung einer zufälligen Schwingungsumgebung verwendet, wie sie in militärischen und kommerziellen Prüfnormen definiert ist.